 DPC Latency Checker is a free tool that shows in real-time how quickly your system reacts to the tasks it has to complete. DPC stands for Deferred Procedure Call, which is a Windows mechanism that allows high-priority tasks to defer lower-priority tasks for later execution. For example, device drivers are high-priority tasks that need to be processed right away before any other task. If a device has an improper driver this operation is going to take more time than usual and it’s going to slow down the system which will lead to interruptions in real-time audio and video streams. In this article I will show you how you can use DPC Latency Checker to find out if you have a device driver problem and, if any, how to fix it.
DPC Latency Checker is a free tool that shows in real-time how quickly your system reacts to the tasks it has to complete. DPC stands for Deferred Procedure Call, which is a Windows mechanism that allows high-priority tasks to defer lower-priority tasks for later execution. For example, device drivers are high-priority tasks that need to be processed right away before any other task. If a device has an improper driver this operation is going to take more time than usual and it’s going to slow down the system which will lead to interruptions in real-time audio and video streams. In this article I will show you how you can use DPC Latency Checker to find out if you have a device driver problem and, if any, how to fix it.
First, you need to download DPC Latency checker. It’s a small 310KB file, that doesn’t even need installation. Then download the tutorial on how to use DPC Latency Checker. The tutorial explains very well how to use the tool, how to interpret the results and what solutions you have in case problems are encountered.
Note: DPC Latency Checker measures the response time of your system. The response time is influenced by any other application that is currently running on your system. For an accurate result, we recommend you to close all applications before launching DPC Latency Checker. If you run this tool while there are applications open you will notice that, while you close them, the results will improve.
The screenshot below is taken on a system that doesn’t have any problems.
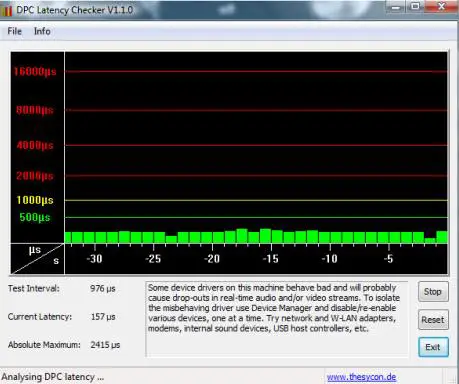
The screenshot below is taken on a system that has a device driver problem.
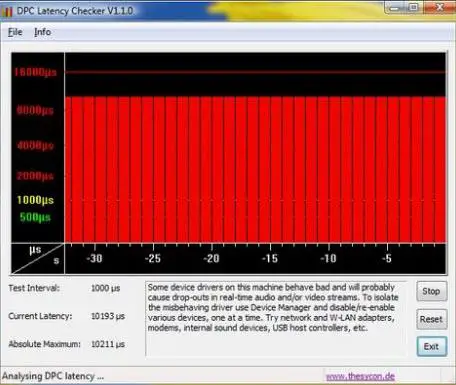
Unfortunately DPC Latency Checker only shows if there is a device driver problem, not which driver is causing the problem. You will have to manually disable and then re-enable each device driver from Device Manager. Make sure you carefully read the DPC Latency Checker tutorial about which drivers you should disable first and which drivers you should not disable.
If you know any other tools that could help troubleshoot driver problems don’t forget to mention them in a comment. Also, if you find any problematic drivers let us know.
Related articles:
Uninstall the driver of a hardware component
Check your system health with the Reliability and Performance Monitor
Check your System Stability Index
Solve your computing problems with Problem Reports and Solutions
Windows Memory Diagnostics Tool


tenho problema com a placa
tenho problema com a placa dlink dwl g520, ja usei esse soft, fica vermelhao.
thank you
thank you
First DPCL screen..
Says that max DPC Latency spiked to 2415… you call that a system with no problem?
HIIIII..
my latency is up to 8000..and i tryid to turn of everything in device manager with no effect.. any suggestion??